Base 2 Math and Logic Gates

Binary Base 2 Math

---

Introduction to Binary

• Binary is a number system using two digits: 0 and 1, also known as Base-2
• Binary is the language of computers as electronic circuts use two states: 0 representing OFF, and 1 representing ON
• Each digit in a binary number is called a bit
  • A group of bits can represent anything from numbers, to text, to images, and more. All of these are represented in binary form

Why Binary?

• Binary makes it much easier to compress, store, and transfer data (data being numbers, texts, images, sounds, etc)
• Does this by using file formats such as JPEG, PNG, BMP, etc.
  • These are just long sequences of 0s and 1s.
• Binary is the most reliable way to store and process data using electronic components.

Comparing Number Systems

Number	Decimal (Base 10)	Binary (Base 2)	Octal (Base 8)	Hexadecimal (Base 16)
0	0	0	0	0
1	1	1	1	1
2	2	10	2	2
3	3	11	3	3
4	4	100	4	4
8	8	1000	10	8
15	15	1111	17	F

Why Do We Use Other Bases?

• Octal (Base 8) → Used in early computing systems.
• Hexadecimal (Base 16) → Used in memory addresses, color codes, and low-level programming because it’s more compact than binary.

Binary Number System

• Each binary digit (bit) represents an increasing power of 2, from right to left.

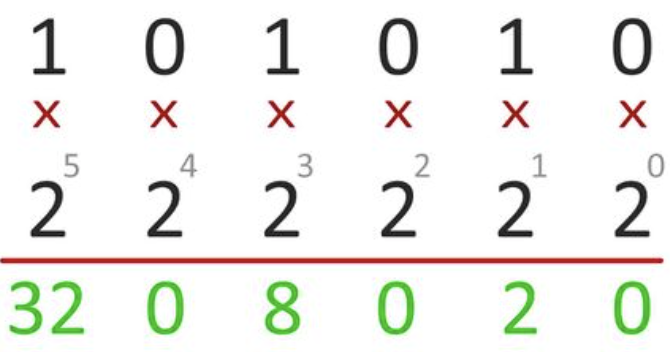
As you can see from this image, you multiply each bit by 2^(n-1), n representing the place value. Once you do that, you add up everything and get the decimal number. So for this example shown in the image, the binary number 1010101 comes out to be 42 in decimal form.

Converting Decimal to Binary

Here are the simple steps to convert decimal to binary

• 1. Divide the decimal number by 2.
• 1. Record the remainder (0 or 1).
• 1. Repeat until you reach 0.
• 1. Read from bottom to top.

Example: Convert 13 to binary

13 ÷ 2 = 6 remainder 1 6 ÷ 2 = 3 remainder 0 3 ÷ 2 = 1 remainder 1 1 ÷ 2 = 0 remainder 1

Binary result: 1101

---

Popcorn Hack 1: Examples for Identifying Binary

1. Example 1:
   • Number: 101010
2. Example 2:
   • Number: 12301
3. Example 3:
   • Number: 11001

---

Binary Arithmetic

Here are the simple steps to perform binary arithmetic:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (carry the 1)

Example:

   1101  (13 in decimal)
+  1011  (11 in decimal)
--------
  11000  (24 in decimal)

Binary Subtraction Rules

Here are the simple steps to perform binary subtraction:

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 = 1 (borrow from the left)

Example: 1101 - 1011 = 0010 (2 in decimal)

---

Popcorn Hack 2: Examples for Adding and Subtracting Binary

1. Example 1 (Adding):
   • Binary Numbers: 101 + 110
2. Example 2 (Subtracting):
   • Binary Numbers: 1101 - 1011
3. Example 3 (Adding):
   • Binary Numbers: 111 + 1001

---

Two’s Complement (Negative Numbers)

• Computers store negative numbers using Two’s Complement.
• Binary subtraction and addition use the same circut: computers dont need to separate logic for negative numbers.
• Simply put, twos complement makes math much easier and efficient for computers

Here is the simple steps in converting positive to negative

1. Invert all bits (flip 0s to 1s and 1s to 0s).
2. Add 1 to the result.

Example: Convert 5 (00000101) to -5

1. Flip bits:  11111010
2. Add 1:      11111011  (This is -5 in two’s complement)

---

Left Shift & Right Shift

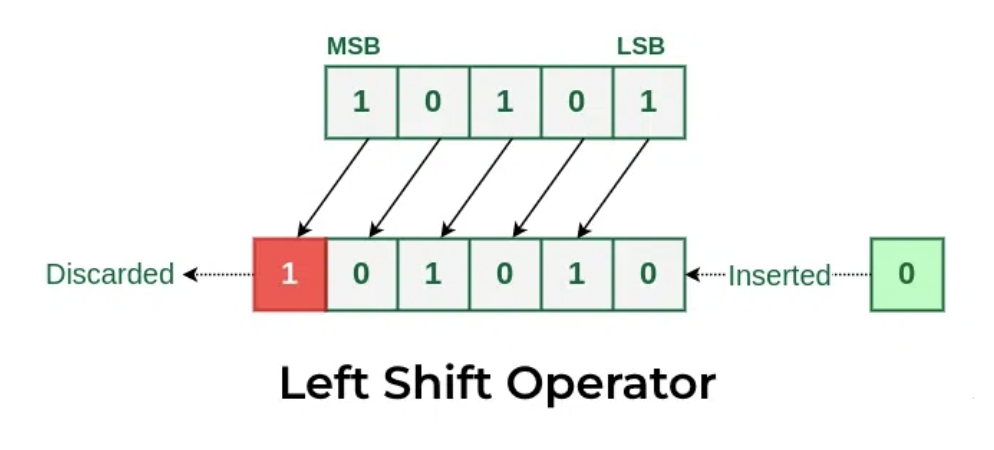
• Left Shift moves all bits to the left and adds a 0 on the right and drops the leftmost bit.
• The result of a left shift: Multiplies the number by 2 for each shift

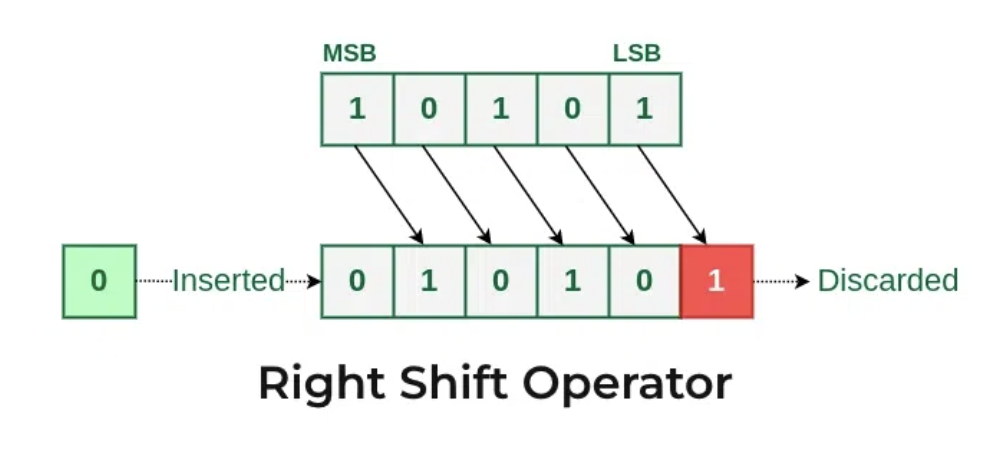
• Right shift moves all the bits to the right and adds a 0 on the left and discards the rightmost bit.
• The result of a right shift: Divides the number by 2 for each shift.

Real-World Applications of Binary Math

Memory Storage

• 1 Bit → Smallest unit of data.
• 1 Byte = 8 Bits (Can store 1 character)
• 1 KB (Kilobyte) = 1024 Bytes
• 1 MB (Megabyte) = 1024 KB
• 1 GB (Gigabyte) = 1024 MB

Binary in Networking

• IP Addresses are stored as binary numbers.
• Example: 192.168.1.1 → 11000000.10101000.00000001.00000001

---

Logic Gates in Python Code

Overview

The following Python function was part of a project submitted by one of our members last trimester. It demonstrates logical operations used in validating a request.

def post(self):
    try:
        # Get request body
        body = request.get_json()

        if not body or 'theme' not in body or 'css' not in body:
            return {"message": "Invalid request. 'theme' and 'css' are required to add."}, 400

        theme = body['theme']
        css = body['css']

        # Create a new theme
        new_theme = Theme(theme=theme, css=css)
        new_theme.create()

        # Return success response
        return new_theme.read(), 201
    except Exception as e:
        return {"message": f"Error adding theme: {str(e)}"}, 500

---

Identification of Logic Gates in the Code

Logical operations are present in the following conditional statement:

if not body or 'theme' not in body or 'css' not in body:

This line applies logic gates to validate the incoming request:

Keyword	Logic Gate Equivalent
not	NOT Gate
or	OR Gate

---

Explanation of the Logic

The condition evaluates three aspects:

• Whether the request body is empty.
• Whether the key 'theme' is missing from the request body.
• Whether the key 'css' is missing from the request body.

If any of these conditions are True, the function returns an error response indicating that the request is invalid.

---

Logic Gates Overview

As you prepare for the AP Computer Science exam, understanding three basic logic gates is crucial:

Gate	Symbol	Python Syntax	Description
AND		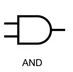A and B	Returns True if both A and B are True; otherwise, returns False.
OR		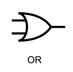A or B	Returns True if at least one of A or B is True; otherwise, returns False.
NOT		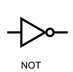not A	Returns the inverse of A; True becomes False and vice versa.

---

Logic Gates Specifics

Important Notes

• 1 represents True
• 0 represents False

AND GATES

Description

An AND gate outputs 1 (true) only if both of its inputs are 1. If any input is 0, the output is 0. This follows the logical conjunction operation.

Truth Table

A	B	Output
0	0	0
0	1	0
1	0	0
1	1	1

Python Syntax

# AND gate example with strings
string1 = "Apples"
string2 = "Bananas"

if string1 == "Apples" and string2 == "Bananas":
    print("True")  # Output: True
else:
    print("False")

# Example where condition is false
string1 = "Apples"
string2 = "Oranges"

if string1 == "Apples" and string2 == "Bananas":
    print("True")
else:
    print("False")  # Output: False

Symbol

---

OR GATES

Description

An OR gate outputs 1 (true) if at least one of its inputs is 1. The output is 0 only when both inputs are 0. It follows the logical disjunction operation.

Truth Table

A	B	Output
0	0	0
0	1	1
1	0	1
1	1	1

Python Syntax

# OR gate example with strings
string1 = "Apples"
string2 = "Bananas"

if string1 == "Apples" or string2 == "Bananas":
    print("True")  # Output: True
else:
    print("False")

# Example where condition is false
string1 = "Oranges"
string2 = "Grapes"

if string1 == "Apples" or string2 == "Bananas":
    print("True")
else:
    print("False")  # Output: False

Symbol

---

NOT GATES

Description

A NOT gate (or inverter) outputs the opposite of its input. If the input is 1, the output is 0, and vice versa.

Truth Table

A	Output
0	1
1	0

Python Syntax

# NOT gate example with strings
string1 = "Apples"

if not string1 == "Apples":
    print("True")
else:
    print("False")  # Output: False

# Example where condition is true
string1 = "Oranges"

if not string1 == "Apples":
    print("True")  # Output: True
else:
    print("False")

Symbol

---

Popcorn Hack

Click to reveal all possible answers

You really thought we would just give you the answers for free; dw i'll update this after the lesson

Homework

Homework Hacks: Binary Converter

Your task is to write a program that converts between decimal and binary numbers.

Instructions:

• Create a function to convert a decimal number to binary.
• Create a function to convert a binary number (as a string) back to decimal.
• Test your functions with different numbers, both positive and negative.

Use the following functions as a starting point:

• A function that takes a decimal number and returns its binary equivalent.
• A function that takes a binary string and returns its decimal equivalent.

Example Input/Output:

• Decimal to Binary: 10 → 1010
• Binary to Decimal: 1010 → 10 Good luck and Code Code Code!

Binary Converter Homework Hack ANSWER, ONLY OPEN WHEN DONE

Click the section below to view the solution:

Show Answer

def decimal_to_binary(decimal):
    return bin(decimal).replace("0b", "")

def binary_to_decimal(binary):
    return int(binary, 2)

# Example usage
decimal_number = 10
binary_number = "1010"

print(f"Decimal {decimal_number} to Binary: {decimal_to_binary(decimal_number)}")
print(f"Binary {binary_number} to Decimal: {binary_to_decimal(binary_number)}")

Finish this MCQ[https://docs.google.com/forms/d/e/1FAIpQLSfu-ukUO9y-X1HOfv3WBBWPCOQg5HzSk31LMrGkGJSO2B6A8g/viewform?usp=header]: